COMPSCI 180 Final Project 1: Pyramid-Based Texture Analysis/Texture; Matching and Generating Texture using Image Pyramids
Aishik Bhattacharyya & Kaitlyn Chen
Introduction:
This project aims to create a synthetic 2D texture based on an input image. The algorithms used in this project follow that of "Pyramid-Based Texture Analysis/Texture". The paper uses a modified laplacian pyramid that adds orientations in the frequency domain to the pyramid. By matching histograms of the input image and noisy image, as well as the oriented laplacian pyramid, the paper generates oriented textures that match the input image’s structure and pixel values. We also used this paper for support.
Get Oriented Filters:
We first need to get the oriented filters, which extract image features (like edges and textures) along specific orientations. Throughout this project we used 4 oriented filters () , unless specified otherwise. Typically, the filters are defined in the frequency domain, as in the paper. However for simplicity we will define the filters in the spatial domain. We used the predefined filters from pyrtools (pt.steerable_filters('sp3_filters')) . A filter tuned to any orientation can be created through a linear combination of the responses of the four basis filters computed at the same location. This property is what allows the pyramid we later construct to be “steerable”/rotation-invariant.

Example Images Convolved with the Oriented Filters:



Steerable/Oriented Pyramid Construction:
Laplacian pyramids do not capture orientated structures in textures since the basis functions are symmetric, so we need to use a steerable pyramid. Steerable pyramids further divides spatial frequency bands into a set of orientation bands. Given an input source texture image, we first split the image into a high frequency and low frequency components. Then we apply bandpass oriented filters to the low frequency image and then downsample, such that each level of the pyramid is constructed from the previous level’s lowpass band. Similarly we can collapse the pyramid since the steerable pyramid is self-inverting.
Histogram Matching:
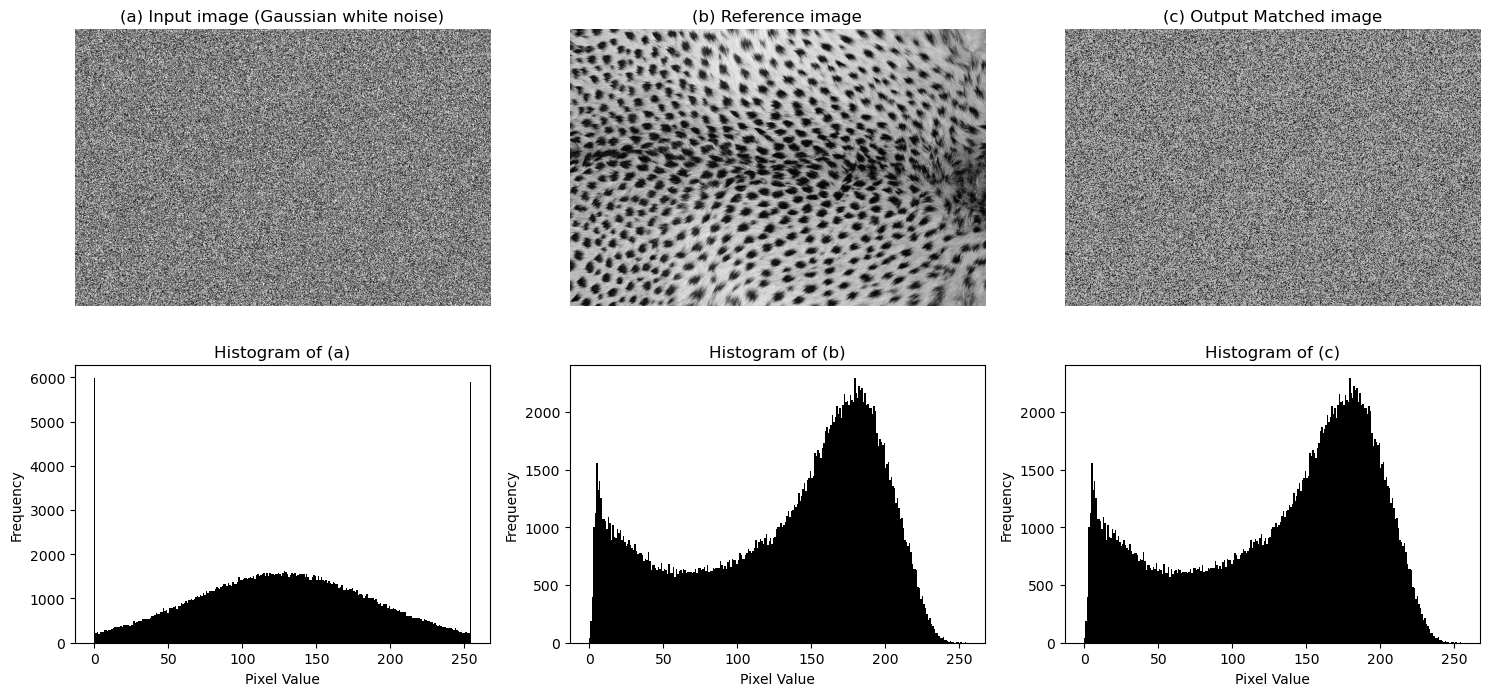
Given an input image and a reference image, histogram matching will change the gray values of the input image to then have the same histogram as the reference image. To do so we sort each images’ pixel values, align the sorted intensities, then map the input image’s pixels to the reference histogram.
Texture Matching (black & white):
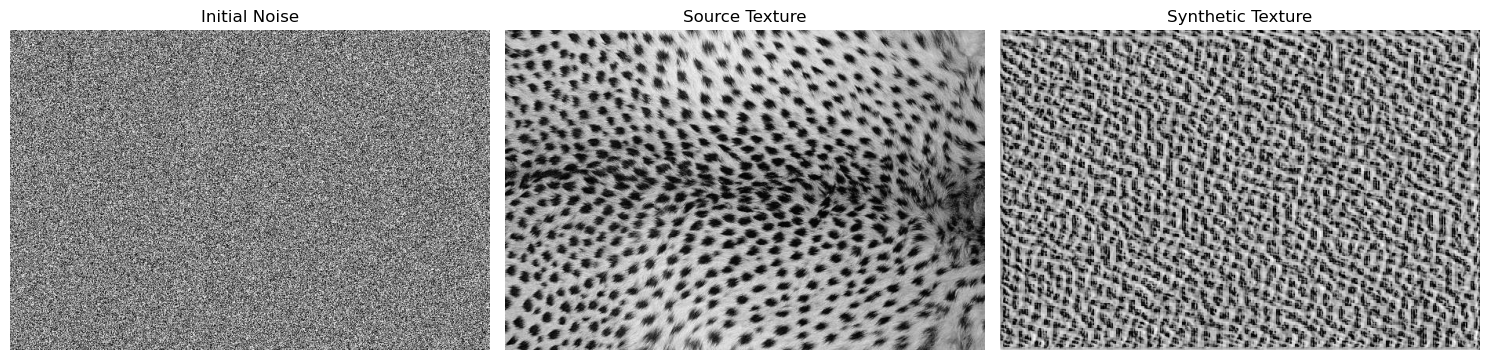
Texture matching aims to modify an input gaussian white noise image to look like the input texture source image. We first match the histograms of the noise image to the source image. We then make pyramids from both the new noise image and texture image. We loop through these two pyramids and match the histograms of each to their corresponding pyramid subbands. We collapse this histogram matched noise pyramid to generate a preliminarly synthetic texture. When we looped through the two pyramids to match histograms, the collapsed image’s histogram then changes so we need iterate through this process, rematching the histograms of the images and the histograms of the pyramids’ subbands. The idea is that after some iterations the output histograms will match that of the source texture.
Example of texture matching:
Adding Color to Texture Matching:
We can not simply treat each RGB channel independent of one another and synthesize them independently, since they are all correlated. Instead we will change the RGB color space to be input adapted so that each independent color channel synthesis yields good results. We create this new RBG color space with principal component analysis (PCA) of the RBG point cloud corresponding to the input source texture. The idea is that in the PCA color space the 3 channels are decorrelated and independent, so we can synthesize them independently.
The source image is first cropped to be a square with dimensions as a power of two, centered around zero, and its covariance matrix is used to compute a decorrelation transformation. We can then synthesize synthetic textures for each of the 3 decorrelated RBG channels. This gives the output synthetic textures in PCA color space, so we need to recorrelate the channels using the inverse transformation and recentering the image to match that of the source image. We can simply stack these channels to give our final outputted synthesized color texture.
Example results all using 5 iterations in texture matching and 4 orientation filters:
For the failure examples I think they failed since the images were not homogeneous textures. Also the textures may be locally oriented but the dominant orientation is different.
Bells & Whistles - Hypertuning:
First we will tune the number of pyramid levels keeping the number of iterations 5 and using 4 orientation filters. We can see that the number of pyramid levels improves it up until a certain point, but will get worse. We can see that tuning the pyramid levels we can achieve better results


Here we will tune the number of iterations (keeping the number of pyramid levels 3 and 4 orientation filters). We can see that similar to the levels tuning above after a certain point the accuracy diminishes. Increasing the number of iterations is computationally exprensive


Here we will tune the number of orientation filters (keeping number of iterations = 3 and number of pyramid levels = 3). The orientation filters will be defined by the pyrtools functions.